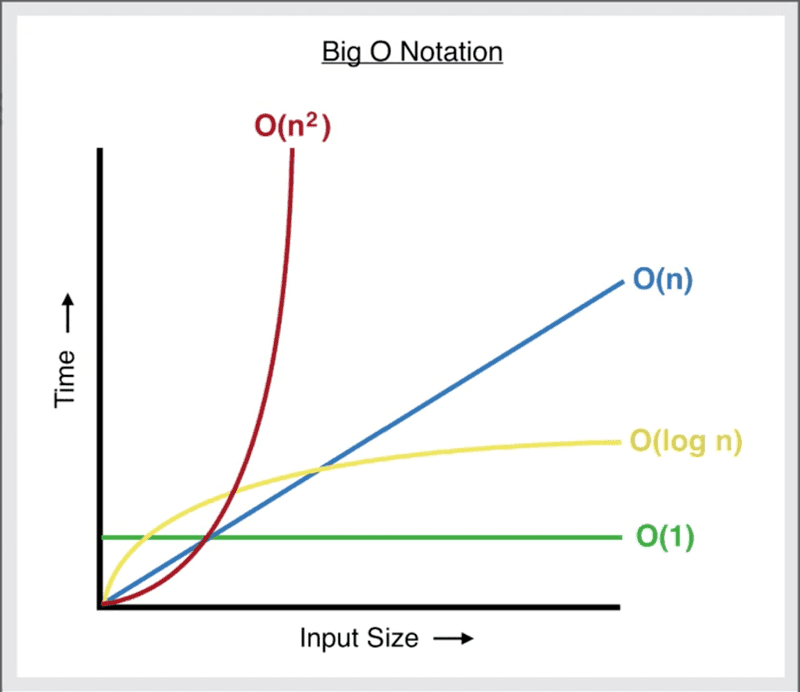
Big-O 표기법이란?

점근 표기법(asymptotic notation)

점근 표기법은 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법입니다. **알고리즘의 복잡도를 단순화(도식화)**할 때나 무한급수의 뒷부분을 간소화할 때 쓰입니다. (위키백과)

Big O 표기법 은 대표적인 점근 표기법중 하나로 어떠한 알고리즘이 최악의 경우를 기준으로 어느정도의 효율성을 보일 것인가를 예측하는 표기법입니다. 어떤 알고리즘을 f(n)이라 하고, 이를 Big-O 표기법으로 표현하면 O(f(n))으로 표현됩니다.

Big-O 복잡도

Big O 로 정의하는 복잡성에는 두가지가 존재합니다.

시간 복잡도
공간 복잡도

시간 복잡도는 대부분의 경우 어떤 알고리즘이 최악의 경우 실행 시간이 어떻게 분포될지를 나타냅니다. 하지만 실행 시간 그 자체를 계산하는 것이 아니라, 연산이 몇 번 이루어지는 가를 계산합니다. 거의 대부분의 경우 실행 시간과 비례합니다.

공간 복잡도는 프로그램을 실행시킨 후 그 프로그램이 종료될 때 까지 필요로 하는 자원 공간을 계산합니다. 즉 메모리 효율을 계산하는 것이라 생각하면 편합니다.

이 글에서는 비교적 자주 쓰이는 시간 복잡도에 대해서만 서술했습니다.

O(1) ⇒ O(n) ⇒ O(n²) ⇒ O(log n) 순서로 예시를 작성했습니다.

일반적인 예시

O(1)

function example1(n) {
  return n + n;
}

example1 은 입력이 1개이며 n의 값에 무관하게 한 번의 연산만 진행합니다. 상수 시간이라고 합니다.

O(n)

function example2(n) {
  for (let i = 0; i < n; i++) {
    console.log(i);
  }
}

example2 는 입력 n번만큼 반복하여 연산합니다. 선형 시간, 혹은 직선적 시간이라고 합니다.

O(n²)

function example3(n) {
  for (let i = 0; i < n; i++) {
    console.log(i);
    for (let j = 0; j < n; j++) {
      console.log(j);
    }
  }
}

example3 는 입력 n의 제곱만큼 연산합니다. 2차 시간이라고 합니다.

번외 : O(n³)

function example4(n) {
  for (let i = 0; i < n; i++) {
    console.log(i);
    for (let j = 0; j < n; j++) {
      console.log(j);
      for (let k = 0; k < n; k++) {
        console.log(k);
      }
    }
  }
}

example4 는 O(n³), 3차 시간 복잡도의 예

O(log n)

function example5(n) {
  for (let i = 0; i < n; i * 2) {
    console.log(i);
  }
}

example5 는 2의 2승(2²)부터 n승까지의 항목을 출력하는 함수입니다. Big-O 표기법은 최악의 경우를 기준으로 한다는 점을 상기해보면, n 입력 값이 천만이라 가정해도 log₂(10,000,000)은 23.253... 이기 때문에 23번만 값을 출력합니다.

Big-O 표기법 규칙

개발할 때 위와같은 간단한 반복문만 사용하지는 않습니다. Big-O 표기법에는 더 복잡한 구조의 알고리즘의 시간 복잡도를 계산할 수 있도록 돕는 규칙이 있습니다. 여러가지 규칙이 있지만 이글에선 자주 사용되는 4가지 법칙만 살펴보겠습니다.

계수 법칙 : 상수 제거하기
합의 법칙 : 빅오 더하기
곱의 법칙 : 빅오 곱하기
다항 법칙 : 빅오의 k승

계수 법칙 상수 제거하기

Big-O 표기법에선 입력 크기와 연관되지 않은 상수를 무시합니다.

function example6(n) {
  let count = 0;
  for (let i = 0; i < n; i++) {
    count += i;
  }
  count *= 100; // 1번 지점
  count /= 100; // 2번 지점
  return count;
}

example6 는 n번만큼 반복한 후 추가로 곱하기(*) 연산과 나누기(/) 연산을 합니다. 여기서 마지막 두번의 연산(1,2번 지점)이 위에서 언급한 상수 가 됩니다. 1, 2번 지점의 코드가 없다면 example6 는 f(n) = n 으로 표현할 수 있습니다. 1, 2번 지점의 코드를 포함한다면 example6 는 f(n) = n + 2 로 표현됩니다. 하지만 계수 법칙에 따라 상수를 제거(혹은 제외)함으로 Big-O 표기법으로 표현하면 O(n)이 됩니다.

이 법칙은 곱셈에서도 유효합니다.

function example7(n) {
  let count = 0;
  for( let i = 0; < n * 10; i++ ) {
    count += i;
  }
  return count;
}

example7 은 n * 10번 반복하여 연산합니다. 10배라면 꽤 큰 숫자로 보입니다. 하지만 Big-O 표기법은 최악의 경우를 기준으로 한다는 점을 기억해야 합니다. n을 무한대 또는 아주 큰 수라고 생각하면 10배로 연산한다고 해서 크게 달라지는 점은 없습니다. Big-O 표기법은 n(입력값)에 비례하여 알고리즘이 어느정도의 효율성을 보이느냐를 따지는 지표이므로 이와같은 상수는 큰 영향을 주지 못합니다.

합의 법칙 빅오 더하기

합의 법칙은 시간 복잡도를 더할 수 있다는 것입니다. 두개 이상의 여러 알고리즘을 보유한 상위의 알고리즘이 있고, 이 알고리즘을 Big-O 표기법으로 표현하고 싶을 경우가 있습니다. 합의 법칙은 이런 경우에 적용할 수 있습니다.

function example8(n) {
  for (let i = 0; i < n; i++) {
    // 1번 지점
    console.log(i);
  }
  for (let j = 0; j < n * 2; j++) {
    // 2번 지점
    console.log(j);
  }
}

1번 지점은 n번만큼 반복하여 f(n) = n 입니다. 2번 지점은 n * 2번 반복하여 f(n) = 2n 입니다. 이를 합하게 되면 f(n) = 6n 이 됩니다. 이제 여기에 계수 법칙을 적용하게 되면 O(n) = n 으로 표현할 수 있습니다.

곱의 법칙 빅오 곱하기

곱의 법칙은 합의 법칙과 마찬가지로 시간 복잡도를 곱할 수 있다는 것입니다.

function example9(n) {
  let count = 0;
  for (let i = 0; i < n; i++) {
    ++count;
    for (let j = 0; j < 2 * n; j++) {
      ++count;
    }
  }
  return count;
}

example9 함수는 f(n) = n * 2n 입니다. 수식에 따라 시간 복잡도를 곱하게 되면 f(n) = 2n² 가 되고, 여기에 계수 법칙을 적용하면 최종적으로 O(n) = n² 로 표현할 수 있습니다.

다항 법칙 빅오의 k승

다항 법칙은 곱의 법칙과 비슷한 맥락으로 이해할 수 있습니다. 시간 복잡도가 여러개의 항(다항)을 가지고 있을 때 동일한 다항 차수를 지닌 빅오 표기법을 지님을 나타냅니다.

function example10(n) {
  let count = 0;
  for (let i = 0; i < n * n; i++) {
    ++count;
  }
  return count;
}

example10 함수에서 f(n) = n * n = n² 입니다.

Ksss Blog

Big-O 표기법 (Big-O Notation)